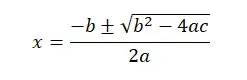pcarballosa
Nivel 5
- 1,226
- 1,374
En este corto tutorial en varias partes, vamos a ir viendo poco a poco y de un modo lo más resumido posible, cómo podemos hacer un intérprete de ecuaciones matemáticas (una especie de intérprete de un lenguaje de programación bastante limitado).
En todo caso, en esta primera parte nada más daré la idea a modo de introducción, y también me servirá para saber si este tema es de interés para algunos a pesar entre otras cosas de su relativa dificultad, lo cual me gustaría conocer por lo menos a través de un comentario, porque si resulta más o menos de interés, después podré crear todas las partes subsiguientes del texto, donde programaré el intérprete hasta terminarlo, y en caso contrario, mejor no perder tiempo en eso dado no le serviría a nadie.
Es decir, cuando terminemos de hacer todo lo necesario, si por fin nos ponemos en ello, podremos tomar una fórmula como la del área de una esfera:
En todo caso, en esta primera parte nada más daré la idea a modo de introducción, y también me servirá para saber si este tema es de interés para algunos a pesar entre otras cosas de su relativa dificultad, lo cual me gustaría conocer por lo menos a través de un comentario, porque si resulta más o menos de interés, después podré crear todas las partes subsiguientes del texto, donde programaré el intérprete hasta terminarlo, y en caso contrario, mejor no perder tiempo en eso dado no le serviría a nadie.
Es decir, cuando terminemos de hacer todo lo necesario, si por fin nos ponemos en ello, podremos tomar una fórmula como la del área de una esfera:
convertirla en una cadena de caracteres conteniendo la misma ecuación matemática en forma de texto:
Area=4*Pi*Sqr(r);
y entonces, una vez asignado un valor numérico a la variable “r” y a la constante “Pi” (la cual se representará como una variable), evaluar la cadena de caracteres y obtener un resultado numérico en la variable de salida “Area”.
La ecuación en la cadena de caracteres, como pueden darse cuenta por lo expuesto antes, deberá ser terminada con un carácter “;” (como se hace en C y otros lenguajes), y esto se debe en gran parte a lo comentado a continuación.
El intérprete de ecuaciones hecho por nosotros también deberá ser capaz de procesar una cadena conteniendo no solo una sino un número indeterminado de ecuaciones, y por eso usaremos un carácter “;” como terminación o separador, con la intención de poder reconocer las distintas partes o ecuaciones descritas en la cadena de caracteres o de texto sin vernos en la necesidad de introducirlas como diferentes líneas.
Por lo demás, las ecuaciones en la cadena podrían no tener relación entre ellas, o sí podrían tenerla y hasta compartir variables, o sea, una misma variable podría usarse en las distintas ecuaciones descritas en la cadena, o una variable de salida ser una de entrada de otra ecuación.
La fórmula cuadrática usada para encontrar la solución de una ecuación de segundo grado podría servirnos de demostración de lo antes dicho (por lo menos para cuando se trata de variables de entrada compartidas por las distintas ecuaciones):
La ecuación en la cadena de caracteres, como pueden darse cuenta por lo expuesto antes, deberá ser terminada con un carácter “;” (como se hace en C y otros lenguajes), y esto se debe en gran parte a lo comentado a continuación.
El intérprete de ecuaciones hecho por nosotros también deberá ser capaz de procesar una cadena conteniendo no solo una sino un número indeterminado de ecuaciones, y por eso usaremos un carácter “;” como terminación o separador, con la intención de poder reconocer las distintas partes o ecuaciones descritas en la cadena de caracteres o de texto sin vernos en la necesidad de introducirlas como diferentes líneas.
Por lo demás, las ecuaciones en la cadena podrían no tener relación entre ellas, o sí podrían tenerla y hasta compartir variables, o sea, una misma variable podría usarse en las distintas ecuaciones descritas en la cadena, o una variable de salida ser una de entrada de otra ecuación.
La fórmula cuadrática usada para encontrar la solución de una ecuación de segundo grado podría servirnos de demostración de lo antes dicho (por lo menos para cuando se trata de variables de entrada compartidas por las distintas ecuaciones):
La ecuación matemática mostrada arriba se puede traducir en la cadena de caracteres listada a continuación, en la cual como se ha dicho son compartidas por lo menos las variables usadas como entrada o como parámetros:
X1=(-b+Sqrt(Sqr(b)-4*a*c))/(2*a);X2=(-b-Sqrt(Sqr(b)-4*a*c))/(2*a);
En fin, nuestro intérprete de ecuaciones matemáticas deberá ser capaz de tomar una cadena de texto con una ecuación o una serie de ecuaciones de parte del usuario, y como su nombre lo indica, interpretarla; y en este sentido, como se ha dicho antes, funcionaría como un intérprete de un lenguaje de programación bastante limitado, uno nada más capaz de reconocer ciertos símbolos y hacer cálculos numéricos con ellos.
Por lo general, cuando se diseña un lenguaje de programación, como primer paso se suele especificar su gramática, o las reglas por las cuales nos guiamos (o se guían las herramientas como BISON y YACC dedicadas a generar de forma automática código en C para un analizador sintáctico) para reconocer un programa, saber si es válido, y detectar los posibles errores a la hora de compilarlo o interpretarlo.
Nota: En este tutorial no se usarán herramientas como YACC, todo lo haremos como se dice a palo, escribiendo todo el código a mano.
En forma bastante simplificada, porque el procesamiento de un programa escrito en un lenguaje de alto nivel como el llevado a cabo por un intérprete o un compilador puede llegar a ser complicado, podemos decir éste por lo general se hace con la colaboración de diferentes procedimientos bien delimitados.
El texto fuente del programa escrito en un lenguaje de alto nivel es recorrido en primer lugar por el Analizador lexicográfico, el cual se limita a garantizar se hayan utilizado en su escritura sólo los símbolos que se consideran válidos según la gramática, y también identifica cada uno de los elementos denominados como tokens o lexemas a medida se los va reconociendo (si se trata de una palabra reservada, de un identificador, de un operador, etc.).
En un momento posterior (o por lo menos así se hacía antes debido a las limitaciones de memoria de las computadoras porque ahora cada proceso puede funcionar de una manera más colaborativa) las tablas de símbolos y la secuencia de tokens detectados durante el análisis lexicográfico son pasadas a un Analizador sintáctico, esta vez para llevar a cabo la creación del árbol de sintaxis y detectar todos los errores de esa índole (sintácticos), también según lo dictado por la gramática del lenguaje de programación de alto nivel a ser procesado.
Por último, en caso de no detectarse errores en ninguno de los pasos mencionados, los resultados obtenidos en el paso anterior le sirven como entrada a otra de las partes del compilador o intérprete denominada Analizador semántico, encargada esta vez de encontrar errores en la semántica, mucho más difíciles de detectar puesto estos son errores en el sentido del programa (se busca conocer si ese programa va a hacer lo esperado, lo cual resulta un poco más complicado como se podrán imaginar).
El proceso casi terminaría ahí en un intérprete, puesto en este no es necesario llegar a la generación de código nativo de un procesador determinado, y sólo se procedería a ejecutar las instrucciones (a menos se trate de un intérprete de P-Code o Bytecode y se necesite convertir el programa primero a uno de estos), sin embargo, un compilador real seguiría su proceso para convertir el texto fuente en un texto en un lenguaje más básico como ensamblador, optimizando el código resultante, y compilar ese código en el lenguaje ensamblador para obtener un programa en código nativo terminado, una vez se haya enlazado el código objeto con las bibliotecas de funciones necesarias.
Por fortuna, nosotros no nos veremos en la necesidad de hacer todo lo descrito para poder crear nuestro intérprete básico de ecuaciones matemáticas, porque eso podría tomarnos bastante en caso de hacerlo con código a mano, aun cuando como se deben imaginar por lo dicho, o no hubiera comentado nada de esto, sí vamos a describir más o menos la parte de la gramática imprescindible para representar las expresiones matemáticas, porque a pesar de todo, en un intérprete de ecuaciones sí se necesita de por lo menos una forma rudimentaria de análisis lexicográfico, y también de un análisis sintáctico suficiente, o en caso contrario no podríamos detectar ningún error en alguna de las ecuaciones.
En resumen, esto es todo para esta parte del tutorial, la cual como mencioné era nada más una especie de introducción del tema para manifestar la idea, y también serviría para conocer si alguien se interesa en estos asuntos poco prácticos.
En la siguiente entrega procederemos a describir la gramática en forma BNF (Backus-Naur Form) necesaria para hacer nuestro intérprete, llamada de esa manera por haber sido inventada por John W. Backus y después modificada por Peter Naur, el primero de ellos creador de lenguaje FORTRAN (primer lenguaje de alto nivel conocido) junto a un grupo de programadores.
Por último, en la entrega o parte final, tal vez a su vez dividida en distintas partes para no hacerla demasiado grande, implementaremos el intérprete usando código BASIC, o si lo prefieren usando otro lenguaje como C, C++, o Pascal, etc., no obstante, la idea de hacerlo usando BASIC es permitirnos utilizar lo creado para hacer una calculadora científica para DOS con una interfaz gráfica de usuario (ver ¿Cómo hacer una calculadora con interfaz gráfica para DOS?), esta vez una calculadora capaz de interpretar ecuaciones introducidas por un usuario en vez de llevar a cabo sólo cálculos más básicos.
Por todo esto, si nadie propone otro lenguaje y se hace con BASIC, los interesados es posible necesiten por lo menos QB64, un compilador BASIC compatible con Microsoft QuickBasic 4.5 pero hecho para correr en un Windows moderno de 64 bits (y crear un programa para un sistema como ese).
Por lo pronto, si algo de esto les resultara de interés a pesar de su, como les he dicho, relativa complejidad, y de no ser para nada útil si lo viéramos desde un punto de vista comercial, espero recuerden comentarlo para enterarme y poder seguir elaborando el tutorial, porque así, aun cuando no se gane nada material con hacerlo o estudiarlo, nos serviría para instruirnos un poco en estos temas de los parsers de ecuaciones matemáticas.
Por lo general, cuando se diseña un lenguaje de programación, como primer paso se suele especificar su gramática, o las reglas por las cuales nos guiamos (o se guían las herramientas como BISON y YACC dedicadas a generar de forma automática código en C para un analizador sintáctico) para reconocer un programa, saber si es válido, y detectar los posibles errores a la hora de compilarlo o interpretarlo.
Nota: En este tutorial no se usarán herramientas como YACC, todo lo haremos como se dice a palo, escribiendo todo el código a mano.
En forma bastante simplificada, porque el procesamiento de un programa escrito en un lenguaje de alto nivel como el llevado a cabo por un intérprete o un compilador puede llegar a ser complicado, podemos decir éste por lo general se hace con la colaboración de diferentes procedimientos bien delimitados.
El texto fuente del programa escrito en un lenguaje de alto nivel es recorrido en primer lugar por el Analizador lexicográfico, el cual se limita a garantizar se hayan utilizado en su escritura sólo los símbolos que se consideran válidos según la gramática, y también identifica cada uno de los elementos denominados como tokens o lexemas a medida se los va reconociendo (si se trata de una palabra reservada, de un identificador, de un operador, etc.).
En un momento posterior (o por lo menos así se hacía antes debido a las limitaciones de memoria de las computadoras porque ahora cada proceso puede funcionar de una manera más colaborativa) las tablas de símbolos y la secuencia de tokens detectados durante el análisis lexicográfico son pasadas a un Analizador sintáctico, esta vez para llevar a cabo la creación del árbol de sintaxis y detectar todos los errores de esa índole (sintácticos), también según lo dictado por la gramática del lenguaje de programación de alto nivel a ser procesado.
Por último, en caso de no detectarse errores en ninguno de los pasos mencionados, los resultados obtenidos en el paso anterior le sirven como entrada a otra de las partes del compilador o intérprete denominada Analizador semántico, encargada esta vez de encontrar errores en la semántica, mucho más difíciles de detectar puesto estos son errores en el sentido del programa (se busca conocer si ese programa va a hacer lo esperado, lo cual resulta un poco más complicado como se podrán imaginar).
El proceso casi terminaría ahí en un intérprete, puesto en este no es necesario llegar a la generación de código nativo de un procesador determinado, y sólo se procedería a ejecutar las instrucciones (a menos se trate de un intérprete de P-Code o Bytecode y se necesite convertir el programa primero a uno de estos), sin embargo, un compilador real seguiría su proceso para convertir el texto fuente en un texto en un lenguaje más básico como ensamblador, optimizando el código resultante, y compilar ese código en el lenguaje ensamblador para obtener un programa en código nativo terminado, una vez se haya enlazado el código objeto con las bibliotecas de funciones necesarias.
Por fortuna, nosotros no nos veremos en la necesidad de hacer todo lo descrito para poder crear nuestro intérprete básico de ecuaciones matemáticas, porque eso podría tomarnos bastante en caso de hacerlo con código a mano, aun cuando como se deben imaginar por lo dicho, o no hubiera comentado nada de esto, sí vamos a describir más o menos la parte de la gramática imprescindible para representar las expresiones matemáticas, porque a pesar de todo, en un intérprete de ecuaciones sí se necesita de por lo menos una forma rudimentaria de análisis lexicográfico, y también de un análisis sintáctico suficiente, o en caso contrario no podríamos detectar ningún error en alguna de las ecuaciones.
En resumen, esto es todo para esta parte del tutorial, la cual como mencioné era nada más una especie de introducción del tema para manifestar la idea, y también serviría para conocer si alguien se interesa en estos asuntos poco prácticos.
En la siguiente entrega procederemos a describir la gramática en forma BNF (Backus-Naur Form) necesaria para hacer nuestro intérprete, llamada de esa manera por haber sido inventada por John W. Backus y después modificada por Peter Naur, el primero de ellos creador de lenguaje FORTRAN (primer lenguaje de alto nivel conocido) junto a un grupo de programadores.
Por último, en la entrega o parte final, tal vez a su vez dividida en distintas partes para no hacerla demasiado grande, implementaremos el intérprete usando código BASIC, o si lo prefieren usando otro lenguaje como C, C++, o Pascal, etc., no obstante, la idea de hacerlo usando BASIC es permitirnos utilizar lo creado para hacer una calculadora científica para DOS con una interfaz gráfica de usuario (ver ¿Cómo hacer una calculadora con interfaz gráfica para DOS?), esta vez una calculadora capaz de interpretar ecuaciones introducidas por un usuario en vez de llevar a cabo sólo cálculos más básicos.
Por todo esto, si nadie propone otro lenguaje y se hace con BASIC, los interesados es posible necesiten por lo menos QB64, un compilador BASIC compatible con Microsoft QuickBasic 4.5 pero hecho para correr en un Windows moderno de 64 bits (y crear un programa para un sistema como ese).
Por lo pronto, si algo de esto les resultara de interés a pesar de su, como les he dicho, relativa complejidad, y de no ser para nada útil si lo viéramos desde un punto de vista comercial, espero recuerden comentarlo para enterarme y poder seguir elaborando el tutorial, porque así, aun cuando no se gane nada material con hacerlo o estudiarlo, nos serviría para instruirnos un poco en estos temas de los parsers de ecuaciones matemáticas.