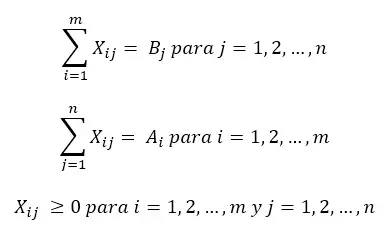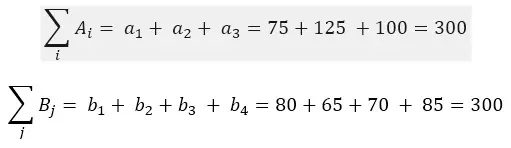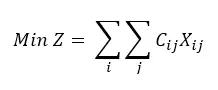pcarballosa
Nivel 5
- 1,226
- 1,374
En este corto texto vamos a ver cómo podemos resolver un problema del transporte utilizando una herramienta a disposición de todos como Microsoft Excel, sin embargo, no se trata del problema de los ómnibus interurbanos, sino de algo más relacionado con la economía de las empresas, los negocios, y hasta un país.
En efecto, en una sociedad moderna, por lo común existe la necesidad de un constante traslado de existencias de un lugar a otro, aun si no tenemos en cuenta cuando se hace más bien nada más con la idea de obtener beneficios a toda costa, causándole daño por pura codicia al maltratado medio ambiente.
En todos lados es necesario llevar arena desde disímiles puntos de extracción hasta los distintos lugares en donde existe una construcción; trasladar artículos desde las distintas fábricas productoras, en donde se los elabora o manufactura, hasta repartirlos en los almacenes y demás sitios en donde satisfacen los deseos de los consumidores; mover caña cortada, reunida previamente en puntos de acopio, hasta los centrales azucareros para su posterior procesamiento.
En fin, la variedad de situaciones de la vida cotidiana en las cuales, como hemos visto, se deben transportar ingentes cantidades de materias primas o mercancías desde un lugar a otro, en verdad podría resultar infinita, y por tanto imposible de enumerar, puesto por lo normal no coinciden casi nunca los sitios donde se obtiene o produce un material, o un producto determinado, y la localización en donde es necesario consumirlo.
En todo caso, aun si se diera la situación y coincidieran los lugares de producción y de consumo, todos debemos de estar de acuerdo en la persistencia de la necesidad de llevar ciertas existencias a otros sitios, puesto por lo general la capacidad de producción de un centro productivo no puede cubrir todas las necesidades del centro de consumo situado a una menor distancia, o por el contrario, dicha capacidad resulta superior en comparación con las necesidades locales y el sobrante debe entregarse en otros lados.
Por causa de todo lo dicho, en la economía de toda empresa tiene preponderancia la toma de decisiones acerca de dónde debería de obtener lo necesario para satisfacer las necesidades de cada una de sus unidades de producción, y hacía dónde debería cada una de estas unidades mandar sus productos semielaborados o terminados de modo se logre hacerlo con los menores costos totales posibles.
El problema del transporte proviene por tanto de ese hecho evidente, conociendo como existe la necesidad de trasportar muchos materiales constantemente tal como lo hemos expuesto. El costo de obtención de una materia prima o de un producto no es igual en dependencia de dónde se lo obtenga o elabora. Pero también este costo puede variar mucho tanto por la distancia entre cada productor y cada consumidor como por el tipo de transporte a utilizar, el estado de los caminos, etc.
La solución del problema es encontrada cuando se conoce, teniendo muchos puntos de envío o producción a los cuales podemos llamar orígenes y muchos puntos de consumo o de recepción a los cuales podemos llamar destinos, la cantidad óptima de un producto o materia prima determinada a transportar desde cada origen a cada destino de modo el costo total de la operación sea mínimo.
El método matemático por excelencia dedicado a la solución de esta clase de problemas en donde se debe determinar las cantidades de un producto a ser transportadas desde un grupo de orígenes a un grupo de destinos, conocidos en su conjunto como Problema del Transporte, es el método simplex desarrollado en la década del cuarenta del pasado siglo XX por el matemático estadounidense George B. Dantzig; aun cuando es necesario mencionar como antes de ser abordado esta clase de problemas en los EE.UU., estaban siendo estudiados en la URSS por Leonid V. Kantorovich, de la universidad de en ese momento Leningrado, porque como deben imaginar, en una economía por naturaleza planificada a gran escala como la de ese país socialista, esta clase de situaciones de optimización se presentó desde un comienzo.
Nota: El matemático soviético Leonid V. Kantorovich recibió un premio Nobel por sus grandes logros en sus investigaciones sobre los problemas de optimización como el comentado.
El problema del transporte es un caso particular de un problema de programación lineal, una rama esta de la matemática orientada a la solución de problemas de optimización.
El proceso para solucionar estos problemas, pasaría por lo normal por la definición del modelo matemático de programación lineal, aun si esto no es estrictamente necesario para resolverlo usando una herramienta como Microsoft Excel.
La definición del modelo matemático de la programación lineal consiste en los siguientes pasos:
1.-Definir la variable de decisión.
2.-Establecer las restricciones del problema.
3.-Establecer la función objetivo.
4.-Resolver el problema por medio del método simplex u otro método disponible.
Todo esto vamos a verlo en más detalle a través de un problema de demostración (el problema ha sido tomado del libro Introducción a la investigación de operaciones).
En este caso se trata de una empresa hipotética nombrada P & T COMPANY uno de los productos más importantes de la cual consiste en chicharos enlatados.
Los chicharos se preparan en tres enlatadoras (orígenes) y después se mandan usando camiones a cuatro almacenes de distribución (destinos).
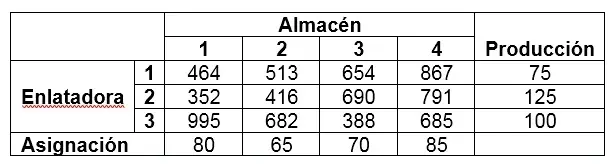
La empresa conoce los costos asociados a enviar cada carga de camión desde uno de los orígenes (enlatadora) a cada uno de los destinos (almacén), así como también las capacidades de producción o disponibilidad de cada enlatadora (en cargas de camión) y la asignación o necesidades de cada almacén (también en cargas de camión).
Los datos anteriores están resumidos en la siguiente tabla:
En efecto, en una sociedad moderna, por lo común existe la necesidad de un constante traslado de existencias de un lugar a otro, aun si no tenemos en cuenta cuando se hace más bien nada más con la idea de obtener beneficios a toda costa, causándole daño por pura codicia al maltratado medio ambiente.
En todos lados es necesario llevar arena desde disímiles puntos de extracción hasta los distintos lugares en donde existe una construcción; trasladar artículos desde las distintas fábricas productoras, en donde se los elabora o manufactura, hasta repartirlos en los almacenes y demás sitios en donde satisfacen los deseos de los consumidores; mover caña cortada, reunida previamente en puntos de acopio, hasta los centrales azucareros para su posterior procesamiento.
En fin, la variedad de situaciones de la vida cotidiana en las cuales, como hemos visto, se deben transportar ingentes cantidades de materias primas o mercancías desde un lugar a otro, en verdad podría resultar infinita, y por tanto imposible de enumerar, puesto por lo normal no coinciden casi nunca los sitios donde se obtiene o produce un material, o un producto determinado, y la localización en donde es necesario consumirlo.
En todo caso, aun si se diera la situación y coincidieran los lugares de producción y de consumo, todos debemos de estar de acuerdo en la persistencia de la necesidad de llevar ciertas existencias a otros sitios, puesto por lo general la capacidad de producción de un centro productivo no puede cubrir todas las necesidades del centro de consumo situado a una menor distancia, o por el contrario, dicha capacidad resulta superior en comparación con las necesidades locales y el sobrante debe entregarse en otros lados.
Por causa de todo lo dicho, en la economía de toda empresa tiene preponderancia la toma de decisiones acerca de dónde debería de obtener lo necesario para satisfacer las necesidades de cada una de sus unidades de producción, y hacía dónde debería cada una de estas unidades mandar sus productos semielaborados o terminados de modo se logre hacerlo con los menores costos totales posibles.
El problema del transporte proviene por tanto de ese hecho evidente, conociendo como existe la necesidad de trasportar muchos materiales constantemente tal como lo hemos expuesto. El costo de obtención de una materia prima o de un producto no es igual en dependencia de dónde se lo obtenga o elabora. Pero también este costo puede variar mucho tanto por la distancia entre cada productor y cada consumidor como por el tipo de transporte a utilizar, el estado de los caminos, etc.
La solución del problema es encontrada cuando se conoce, teniendo muchos puntos de envío o producción a los cuales podemos llamar orígenes y muchos puntos de consumo o de recepción a los cuales podemos llamar destinos, la cantidad óptima de un producto o materia prima determinada a transportar desde cada origen a cada destino de modo el costo total de la operación sea mínimo.
El método matemático por excelencia dedicado a la solución de esta clase de problemas en donde se debe determinar las cantidades de un producto a ser transportadas desde un grupo de orígenes a un grupo de destinos, conocidos en su conjunto como Problema del Transporte, es el método simplex desarrollado en la década del cuarenta del pasado siglo XX por el matemático estadounidense George B. Dantzig; aun cuando es necesario mencionar como antes de ser abordado esta clase de problemas en los EE.UU., estaban siendo estudiados en la URSS por Leonid V. Kantorovich, de la universidad de en ese momento Leningrado, porque como deben imaginar, en una economía por naturaleza planificada a gran escala como la de ese país socialista, esta clase de situaciones de optimización se presentó desde un comienzo.
Nota: El matemático soviético Leonid V. Kantorovich recibió un premio Nobel por sus grandes logros en sus investigaciones sobre los problemas de optimización como el comentado.
El problema del transporte es un caso particular de un problema de programación lineal, una rama esta de la matemática orientada a la solución de problemas de optimización.
El proceso para solucionar estos problemas, pasaría por lo normal por la definición del modelo matemático de programación lineal, aun si esto no es estrictamente necesario para resolverlo usando una herramienta como Microsoft Excel.
La definición del modelo matemático de la programación lineal consiste en los siguientes pasos:
1.-Definir la variable de decisión.
2.-Establecer las restricciones del problema.
3.-Establecer la función objetivo.
4.-Resolver el problema por medio del método simplex u otro método disponible.
Todo esto vamos a verlo en más detalle a través de un problema de demostración (el problema ha sido tomado del libro Introducción a la investigación de operaciones).
En este caso se trata de una empresa hipotética nombrada P & T COMPANY uno de los productos más importantes de la cual consiste en chicharos enlatados.
Los chicharos se preparan en tres enlatadoras (orígenes) y después se mandan usando camiones a cuatro almacenes de distribución (destinos).
La empresa conoce los costos asociados a enviar cada carga de camión desde uno de los orígenes (enlatadora) a cada uno de los destinos (almacén), así como también las capacidades de producción o disponibilidad de cada enlatadora (en cargas de camión) y la asignación o necesidades de cada almacén (también en cargas de camión).
Los datos anteriores están resumidos en la siguiente tabla:
Los pasos para la definición del modelo matemático de programación lineal para poder resolver el comentado problema de transporte serían ahora:
1.-Definir la variable de decisión.
Xij - Cantidad de cargas de camión a transportar desde la enlatadora “i” (1 a “m”) al almacén “j” (1 a “n”).
2.-Establecer las restricciones.
Sujeto a:
1.-Definir la variable de decisión.
Xij - Cantidad de cargas de camión a transportar desde la enlatadora “i” (1 a “m”) al almacén “j” (1 a “n”).
2.-Establecer las restricciones.
Sujeto a:
donde:
Ai – es la sumatoria de las disponibilidades de los orígenes (cargas de camión de latas de chícharos producidas por las enlatadoras).
Bj – es la sumatoria de las necesidades de los destinos (cargas de camión de latas de chícharos para satisfacer la demanda de los almacenes).
En este caso particular “m” vale 3 por haber 3 orígenes (enlatadoras), y “n” vale 4 puesto se disponen de 4 destinos (almacenes de distribución).
En adición, es necesario tener en cuenta en un problema de transporte sólo se pueden encontrar una solución factible inicial si la sumatoria de la disponibilidad de todos los orígenes es igual a la sumatoria de las necesidades de todos los destinos, tal cual lo expresan las siguientes ecuaciones.
Ai – es la sumatoria de las disponibilidades de los orígenes (cargas de camión de latas de chícharos producidas por las enlatadoras).
Bj – es la sumatoria de las necesidades de los destinos (cargas de camión de latas de chícharos para satisfacer la demanda de los almacenes).
En este caso particular “m” vale 3 por haber 3 orígenes (enlatadoras), y “n” vale 4 puesto se disponen de 4 destinos (almacenes de distribución).
En adición, es necesario tener en cuenta en un problema de transporte sólo se pueden encontrar una solución factible inicial si la sumatoria de la disponibilidad de todos los orígenes es igual a la sumatoria de las necesidades de todos los destinos, tal cual lo expresan las siguientes ecuaciones.
En caso de resultar iguales las sumatorias se dice el problema está balanceado, como se comentó antes, y de no ser iguales dichas cantidades sería necesario incluir un origen o un destino ficticio con la disponibilidad o la necesidad adecuada, de modo podamos igualar las sumatorias, puesto esto es una condición necesaria para poder resolver el problema usando el método simplex de transporte.
En el presente problema se cumple esa restricción, como pueden ver por las ecuaciones anteriores en donde la sumatoria de la producción o disponibilidades de los orígenes y de las cantidades de asignación o las necesidades de los destinos resultan ser iguales.
3.-Función objetivo.
En el presente problema se cumple esa restricción, como pueden ver por las ecuaciones anteriores en donde la sumatoria de la producción o disponibilidades de los orígenes y de las cantidades de asignación o las necesidades de los destinos resultan ser iguales.
3.-Función objetivo.
donde:
Cij – es el costo de transportar una unidad de carga del origen “i” al destino “j”.
La definición del modelo matemático del problema de transporte, tal como se lo ha hecho en los párrafos anteriores, puede servir también en algunos casos para clarificar dicho problema y notar si es en realidad un problema de transporte, aun si en una demostración tan sencilla como la presente esto no es necesario, y sólo se expone para después representarlo en Microsoft Excel.
Es necesario tener presente como muchos problemas de transporte no consisten en el transporte real de materiales o de artículos de un número de orígenes a un número de destinos sino más bien en problemas de asignación de recursos.
4.-Resolver el problema de transporte usando Solver de Microsoft Excel.
En todo caso, ahora vamos a resolver usando la herramienta Solver propia de Microsoft Excel este problema de transporte de las enlatadoras de chícharo de la empresa P & T COMPANY.
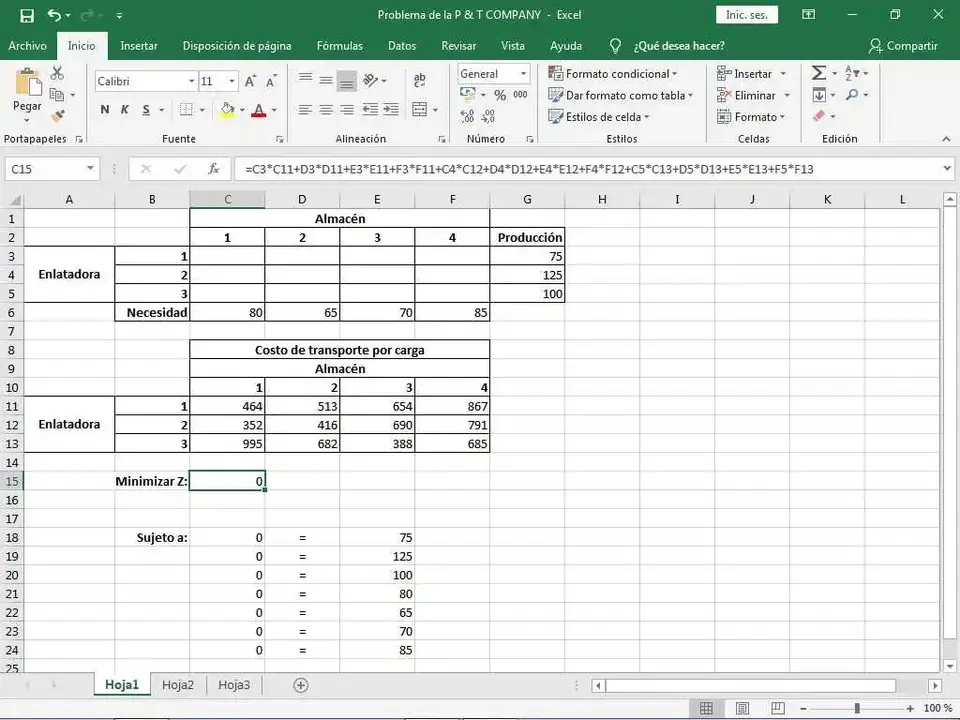
En primer lugar, debemos crear las tablas necesarias como se muestra en la Figura 1 a continuación.
Cij – es el costo de transportar una unidad de carga del origen “i” al destino “j”.
La definición del modelo matemático del problema de transporte, tal como se lo ha hecho en los párrafos anteriores, puede servir también en algunos casos para clarificar dicho problema y notar si es en realidad un problema de transporte, aun si en una demostración tan sencilla como la presente esto no es necesario, y sólo se expone para después representarlo en Microsoft Excel.
Es necesario tener presente como muchos problemas de transporte no consisten en el transporte real de materiales o de artículos de un número de orígenes a un número de destinos sino más bien en problemas de asignación de recursos.
4.-Resolver el problema de transporte usando Solver de Microsoft Excel.
En todo caso, ahora vamos a resolver usando la herramienta Solver propia de Microsoft Excel este problema de transporte de las enlatadoras de chícharo de la empresa P & T COMPANY.
En primer lugar, debemos crear las tablas necesarias como se muestra en la Figura 1 a continuación.
En la figura podemos ver arriba una tabla a la cual podemos llamar de distribución, en esta tabla es donde, como su nombre indica, se obtendrá la distribución óptima, y debajo de esta primera tabla podemos ver otra tabla correspondiente a la tabla de los costes unitarios de transportación expuesta antes.
En adición, en la barra de fórmulas de Microsoft Excel se puede ver la ecuación de la función objetivo por estar la celda correspondiente seleccionada.
Por su parte, las restricciones consisten nada más y nada menos en la implementación de las ecuaciones de las restricciones comentadas antes cuando se hizo la definición del modelo matemático del problema de optimización.
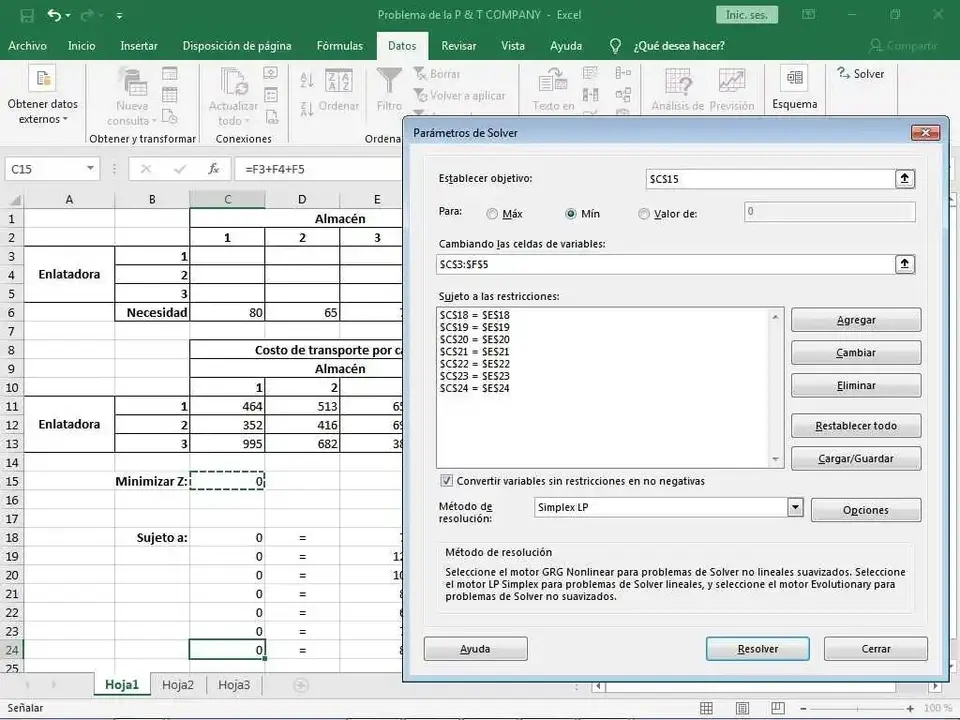
En este momento podemos ir a la ficha Datos de Microsoft Excel y mandar a correr la herramienta Solver (en caso de no mostrarse la herramienta en la mencionada ficha deberá instalarse como un complemento).
En la Figura 2 podemos ver la ventana de la herramienta Solver en la cual han sido establecidos de antemano los distintos parámetros necesarios para obtener la solución del problema una vez demos clic en su botón Resolver.
En adición, en la barra de fórmulas de Microsoft Excel se puede ver la ecuación de la función objetivo por estar la celda correspondiente seleccionada.
Por su parte, las restricciones consisten nada más y nada menos en la implementación de las ecuaciones de las restricciones comentadas antes cuando se hizo la definición del modelo matemático del problema de optimización.
En este momento podemos ir a la ficha Datos de Microsoft Excel y mandar a correr la herramienta Solver (en caso de no mostrarse la herramienta en la mencionada ficha deberá instalarse como un complemento).
En la Figura 2 podemos ver la ventana de la herramienta Solver en la cual han sido establecidos de antemano los distintos parámetros necesarios para obtener la solución del problema una vez demos clic en su botón Resolver.
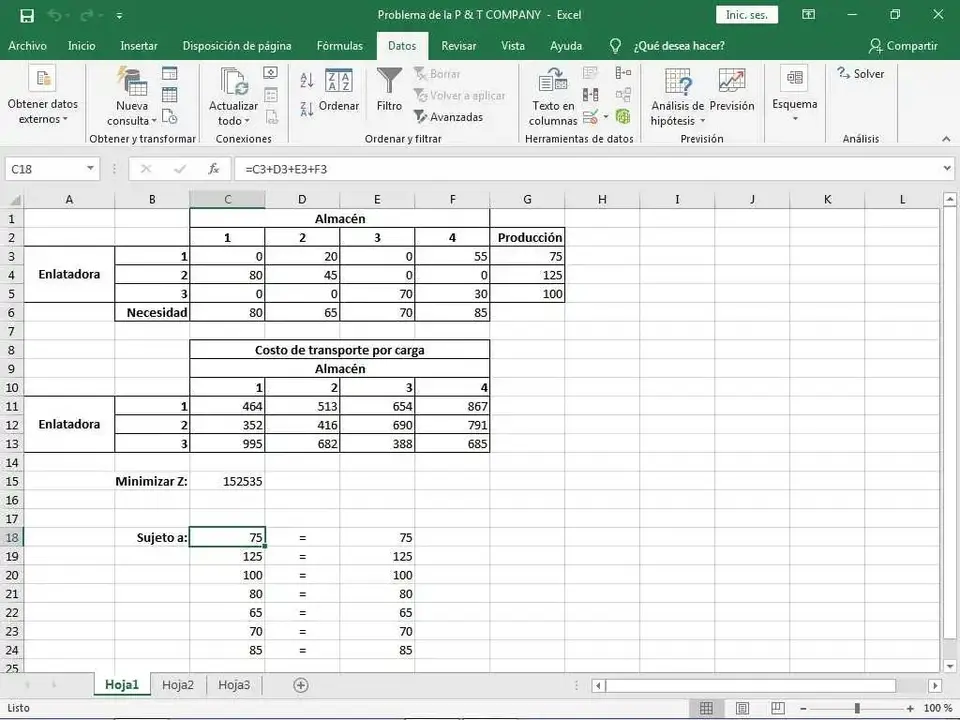
La solución del problema podremos verla en la primera tabla o tabla de distribución, mostrada una vez más en la Figura 3, ahora rellena con los valores correspondientes a las cantidades de cargas de camión a ser enviadas desde cada enlatadora a cada uno de los almacenes de distribución.
En dicha figura también se muestra el valor del costo total mínimo correspondiente a dicha solución óptima del problema de transporte (a la derecha de Minimizar Z).
En resumen, el uso de este método de optimización puede ser extremadamente útil a las empresas, negocios, o incluso un país (si su economía es planificada), si se desea conseguir un importante ahorro de los recursos disponibles y un mejor funcionamiento de su economía, lo cual redunda favorablemente en su capacidad para competir en los mercados.
El libro de Microsoft Excel pueden descargarlo desde: https://drive.google.com/file/d/1-j4zEyOp3JIVvVSH8GiLOlwZD9o2Rv-x/view?usp=sharing
¿Qué otras herramientas para optimizar el funcionamiento de las empresas conocen?
En resumen, el uso de este método de optimización puede ser extremadamente útil a las empresas, negocios, o incluso un país (si su economía es planificada), si se desea conseguir un importante ahorro de los recursos disponibles y un mejor funcionamiento de su economía, lo cual redunda favorablemente en su capacidad para competir en los mercados.
El libro de Microsoft Excel pueden descargarlo desde: https://drive.google.com/file/d/1-j4zEyOp3JIVvVSH8GiLOlwZD9o2Rv-x/view?usp=sharing
¿Qué otras herramientas para optimizar el funcionamiento de las empresas conocen?